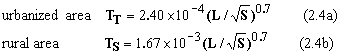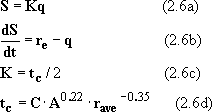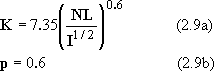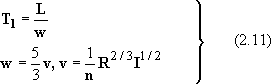Japanese Runoff Methodology

Author: Mitsuo Yamashita following discussion with NJS
Mitsuo Yamashita - Fukuoka University

Selection of rainfall runoff model

There are three rainfall runoff models which are generally used by Japanese hydrological engineers:

• Hydrograph method with rational formula
• Quasi Linear Reservoir Method
• Storage Function Method. (see Fig. 1)

To do the runoff analysis of a specific river basin as a governmental project, one of these models should be selected under the agreement between the hydrological consultant and governmental (or local) authority with consideration of the geographical and hydrological characteristics of the basin (time of concentration, the shape of rising limb of hydrograph and etc.).

Figure 1: Selection of Rainfall Runoff Model

2. Methodology for Application of Rainfall-Runoff Models

2.1 Hydrograph method with rational formula

In Hydrograph method with rational formula, unit time is time of concentration (tc). Hydrograph for every unit time is estimated by Rational Method and they are composed as shown in Fig. 2.1.

This method is used for a runoff analysis of the basins to which Rational Method is applicable.

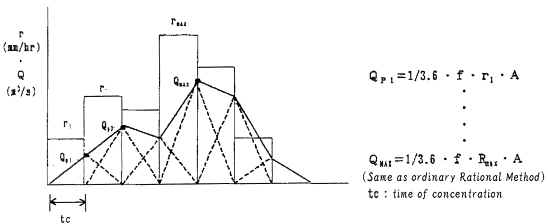
Figure 2: Hydrograph method with Rational Formula Accumulative

2.1.1 Estimation of time of concentration for Hydrograph method with rational formula

In Hydrograph method with rational formula, one of the three method is used for estimation of time of concentration (tc); Kraven method, Uniform Flow velocity Method and PWRI Model.

Kraven Method

In Kraven method, travel time of overland flow (t1) and channel flow (t2) are estimated separately. As for the upper area of 2sq-km in the basin, overland flow is assumed as shown in Fig. 2.2, and the travel time (t1) is assumed as shown in Table 2.1. As for the downstream from there, channel flow is assumed and the travel time (t2) is estimated with (Eq. 2.2) and Table 2.2. The time of concentration (tc) is the sum of these two values.

tc = t1 + t2 (1) where tc: time of concentration (min) t1: travel time of overland flow (min) t2: travel time of channel flow (min)

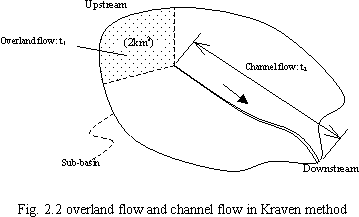
Type of land use	mountainous area	mountainous area with steep slope	urbanized area with drainage system
travel time: t1 (min)	30	20	30

Table 2.1: Typical travel time of overland flow for the upper 2sq-km area (min)

If the catchments area is below 2sq-km, travel time of overland flow (t1) is estimated by multiplying the value of Table 2.1 by (). In this case, travel time of channel flow (t2) is assumed to be zero.

(2) where L: length of channel reach (m) W: velocity of flood wave (m/s) t2: travel time of channel flow (min)

slope of channel: S(m/m)	1/100 and more	1/100～1/200	1/200 and less
Velocity of flood wave: W(m/s)	3.5	3.0	2.1

Table 2.2: slope of channel and the velocity of flood wave

If it is not appropriate to estimate travel time (t2) from the averaged slope of whole channel reach, the channel reach should be divided into several reaches with proper lengths. Then the travel time of each channel reach should be estimated individually and the sum of them is assumed to be t2.

Uniform Flow Velocity Method

In this method, the basic equations for estimation of travel time (t1) and (t2) are the same as the ones in Kraven method. Only the estimation of the velocity of flood wave (W) is different from Kraven method. Instead of Table 2.2, Manning formula (Eq. 2.3) is used to estimate the velocity of flood wave (W).

(3) where n: roughness coefficient of channel R: hydraulic radius of representative river cross section I: averaged slope of river bed(m/m)

Also in this method, if it is not appropriate to estimate the travel time (t2) from the averaged slope of whole channel reach, the channel reach should be divided into several reaches with proper lengths. Then the travel time of each channel reach should be estimated individually and the sum of them is assumed to be t2.

PWRI Model

PWRI model was developed from the relationships between time of concentration T (hr), catchments length L (m) and catchments slope S derived from geographic data and the hydraulic data given by outflow test sites in all over Japan. Equations to estimate concentration time are as follows;

(4) where TT: time of concentration in urbanized area (hr) TS: time of concentration in rural area (hr) L: length between the furthest point in the catchment and the flow measured point S: catchments slope, the ratio of Altitude difference H (m) between the furthest point in the catchment and the flow measured point to the catchments length (L)

Here, this PWRI model is only applicable when the following conditions are met: for urban area, catchment area A is less than 10 sq-km and S is greater than 1/300, while A is less than 50 sq-km and S is greater than 1/300 for rural area.

Yet, when urban area and rural area are mixed up in a catchment, calculate the time of concentration, assuming the whole catchment is occupied only by urban area or rural area, and then use area weighting average method for it (Eq. 2.5).

(5) Where AT = Urban catchment area AS = Rural catchment area TT; time of concentration derived, assuming the whole catchment area is occupied by urbanized area TS; Concentration time derived, assuming the whole catchment area is occupied by rural area

2.1.2 Runoff coefficient (f)

The standard values of runoff coefficient are shown in Table 2.3.

Congested residential area	0.9
General residential area	0.8
Fields, moors	0.6
Rice fields	0.7
Mountains	0.7

Table 2.3 runoff coefficient for Rational Method in Japan

2.2 Quasi Linear Reservoir Method

The basic equations of this method are as follows;

(6) where S: facade storage water depth in a river basin (mm) K: characteristic coefficient of a basin q: runoff depth (mm/h) re: intensity of effective rainfall (mm/h) tc: time of concentration(min) C: coefficient representing the characteristics of a basin rave: averaged intensity of effective rainfall(mm/h) A: area of a basin(sq-km)

(Eq. 2.6d) is called equation of Kadoya. The time of concentration is estimated with this equation in Quasi Linear Reservoir Method. The standard values of C are shown in Table 2.4.

Basin Description	C (characteristics coefficient)
hill slope, mountainous area	290
housing lot before housing	90 - 120
Pasture, golf links	190 - 210
residential area	60 - 90

Table 2.4 standard value of C in equation of Kadoya

2.2.1 Estimation of Effective Rainfall Intensity

One of two methods should be used for estimation of effective rainfall intensity in Quasi Linear Reservoir Method; f1-Rsa Method and Infiltration Capacity Method.

f1-Rsa Method

The concept of f1-Rsa method is depicted as Fig.2.3. In this method, runoff rate is f1 until cumulative rainfall amount reaches to Rsa , and then the runoff rate changes to fsa after that. Usually, the value of fsa is unity.

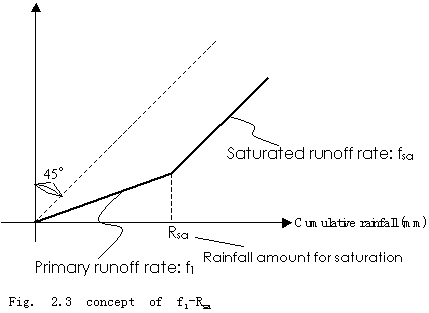
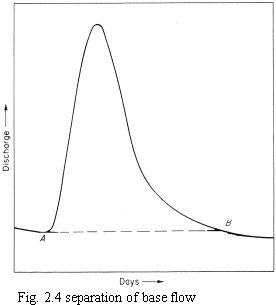
To identify the value of Rsa, the observed hydrographs of several rainfall events should be collected. The base flows of them are separated by using such method as Fig.2.4, and then the accumulated rainfall amounts and accumulated runoff volumes are plotted to a chart. Then the curving point of the regression line will show the value of Rsa.

The standard value of f1 and Rsa are shown in Table 2.5 and Table 2.6. These values can be used for first approximation.

parameter	rural area	urbanized area
f	1	0.5
Rsa(mm)	100	50

Table 2.5 standard values of f1 and Rsa

land use pattern	rice field	farmland	mountain	Residential area 2 degree	Residential area 4 degree
f1	0.0	0.15	0.25	0.7	0.9
Rsa(mm)	50.0	300.0	150.0	55.0	55.0
fsa	1.0	0.6	1.0	1.0	1.0

2 degree and 4 degree represent how urbanized the area are. Please refer to Table 2.7 for the definition.

Table 2.6 standard values of f1 and Rsa for typical land use patterns

Infiltration Capacity Method

The concept of Infiltration Capacity Method is depicted in Fig. 2.5. First of all, in this method, a constant amount of rainfall (rL) is assumed to be substracted as infiltration water from a hyetograph. Next, depression storage (Ia) is removed from the early part of the hyetograph. The residue of the hyetograph is assumed to be effective rainfall.

The values of rL and Ia should be adjusted to match the shape of calculated hydrograph roughly to the observed one by calculating runoff volume (or hydrograph) for each effective rainfall per unit observed rainfall.

2.2.2 Calibration of Parameters

Coefficient C should be calibrated to match the timing of rising limb and peak of the hydrograph to the observed ones.

2.3 Storage Function Method

The basic equations of Storage Function Method are as follows;

(7) where S: facade storage water depth in a river basin(mm) K, p: characteristic coefficients of a basin q: runoff depth (mm/h) re: intensity of effective rainfall (mm/h)

The equation of this method is basically the same as the reservoir function of TRRL method of U.K.

As for the concrete methodology for the calculation, pp.62-76 in the document named as Hydrology for field staff Chapter 5 should be referred.

2.3.1 First Approximation for values of K and p

There are two model parameters in this method; K and p.

 Both of them are derived by changing their values and repeating the calculation enough times so that the calculated hydrograph matches to the observed hydrograph.

There are two method to get the values for the first approximation

• Izzard Constant Method
• Equivalent Roughness Method.

Izzard Constant Method

The basic equations of this method are as follows,

(8) where C: equivalent roughness coefficient of basin (rural area: C=0.12, urbanized area: C=0.012) L: the channel length from the furthest point in the basin and the downstream end of the basin (km) I: the channel slope, the ratio of Altitude difference H (m) between the furthest point in the basin and the downstream end of the basin to the channel length of a basin L*1,000 (m)

Equivalent Roughness Method

The basic equations of this method are as follows,

(9) where L: slope length of a basin (km) I: averaged slope of a basin length (m/m) N: equivalent roughness coefficient of a basin

The standard values of N for typical land use patterns are shown in Table 2.7.

When various land use patterns are mixed up in a basin, use area weighting average method for it.

	land use pattern		value
	water area		0.0
	rice field		2.0
	mountainous area		0.7
	hill slope, pasture, park, golf link, farm land		0.3
	urbanized area (averaged value)		0.03
Degree of Urbanisation	1°	only roads and street gullies are installed bushes and grasses are not removed	0.1
	2°	roads are installed quite well drainage systems are not fully installed	0.05
	3°	half of the planned area to be paved are paved drainage systems are almost installed	0.01
	4°	all of the planned area to be paved are paved drainage systems are fully installed	0.005

Table 2.7 equivalent roughness coefficient (N)

2.3.2 Estimation of Effective Rainfall Intensity

Same as Quasi Linear Reservoir Method described in 2.2.1.

2.3.4 Application of Lag Time

By adding the concept of lag time, the reproductivity of hydrographs is improved in Storage Function Method.

There are two method for the estimation of lag time

• Kimura Method
• Flood Velocity Method.

Kimura Method

Kimura, the developer of Storage Function Method, analyzed the geographical and hydrological data of many Japanese rivers, and proposed the equations to estimate lag time as follows,

(10) where Tl: lag time (hr) L: the channel length from the furthest point in the basin and the downstream end of the basin (km)

Flood Velocity Method

Because, in the middle or small sized river basins, the lag time is calculated to be zero with (Eq. 2.10), the following equations were proposed, which calculate lag time by assuming the averaged cross section and averaged flow velocity.

(11) where v: averaged flow velocity(m/s), R: hydraulic radius of averaged cross section I: the channel slope, the ratio of Altitude difference H (m) between the furthest point in the basin and the downstream end of the basin to the channel length of a basin L (m)

Also, there is a graphical method available by plotting the relationship between facade storage water depth and runoff depth to a chart, but the author omits the description for it in this document.

Generally speaking, when the observed hydrograph is available, the value which matches the calculated hydrograph to the observed one is adopted.

Because Storage Function Method is basically the same as the reservoir function of TRRL method, the method for estimation of lag time in Large Catchment Model of InfoWorks CS may be useful.

2.3.4 Calibration of Parameters

The parameters, K and p, should be calibrated to match calculated hydrograph to the observed one by changing the values and repeating the calculation enough times. If f1-Rsa method is adopted for the estimation of effective rainfall, the value of Rsa should be also calibrated.

As for the relationship between the change of each parameter and its effect, refer the table 2.8.

Table 2.8  Calibration of parameters and its effects

Parameter	Type of Change	Peak flow	Waveform	Peak flow time	Features
K	Larger	Smaller	More gradual	Delay	Appropriate to match the whole shape of a waveform
	Smaller	Larger	Sharper	Faster
P	Larger	Smaller	More gradual	Delay	Appropriate to match the whole shape of a waveform
	Smaller	Larger	Sharper	Faster
T1	Larger	No change	No change	Delay	Appropriate to match the peak flow time
	Smaller	No change	No change	Faster
f1	Larger	Smaller a little	Smaller a little	Delay a little	Appropriate to match the beginning part of a hydrograph
	Smaller	Larger a little	Larger a little	Delay a little
Rsa	Larger	Smaller a little	Smaller a little	Delay a little	Appropriate to represent the differences of catchment wetness
	Smaller	Larger a little	Larger a little	Delay a little

3. Estimation of Effective Rainfall for Several Rainfall Events with Intermissions

The rainfall-runoff models described above are mainly for the peak flow and relating hyetograph and hydrograph. But they do not pay attention to several rainfall events with intermissions as the subject of analysis.

Several methods were proposed which relates antecedent rainfall to the estimation of effective rainfall. For example, there is a method that estimates the cumulative runoff volume with many rainfall by separating base flow with such method as Fig. 2.4, and analyzing the relationship between the cumulative rainfall and runoff volume. Then, based on the results of the analysis, the parameters for the estimation of effective rainfall, such as f1 or r1, are calibrated.

But there is no de facto method.

It might be a good idea to define how long intermissions should be regarded ehough to divide a series of rainfalls into individual events, then assume an equation for the relationship between antecedent rainfall and the value of Rsa in the f1-Rsa method, and update the value of Rsa at every start of single rainfall event in order to derive effective rainfall.

 

Article Copyright: Mitsuo Yamashita ©2006