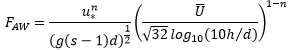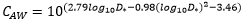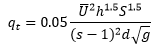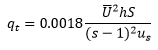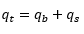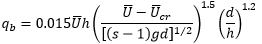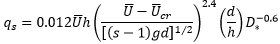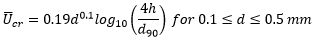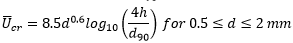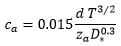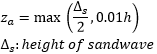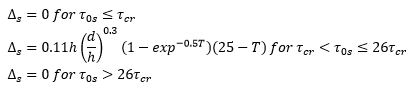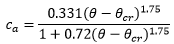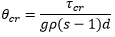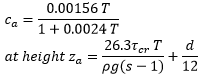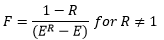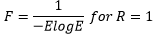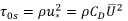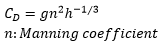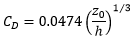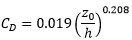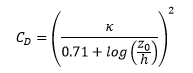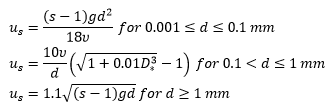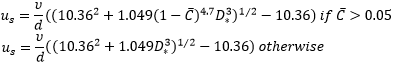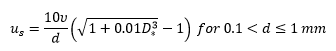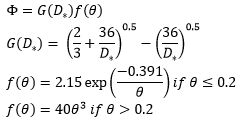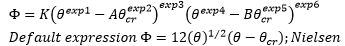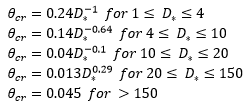2D Sediment Transport

This topic lists the equations used in the calculation of 2D sediment transport when carrying out 2D Water Quality Simulations.

The method of calculation to be used in each case is defined in the Water Quality and Sediment Parameters.

The carrying capacity of the flow is calculated as a volumetric transport rate.

qt: Volumetric transport rate

Volume (m3) of grains moving per unit time (s) per unit width of bed (m); SI units of qt are m2/s

U: depth averaged velocity (m/s)

u*: friction velocity (m/s)

us: sediment settling velocity (m/s)

d: sediment grain diameter (m); d50 unless otherwise stated

h: water depth (m)

s: ratio of sediment and water densities

g: acceleration due to gravity 9.81 m/s2

S: water surface slope

n: kinematic viscosity of water

Dimensionless grain diameter D*:

 

 

 

 

 

where particle mobility FAW:

 

d = d35

Determine the transition exponent, n, the initial motion parameter, AAW, and the coefficient and exponent in the sediment transport function (CAW and m respectively):

 

For 1 < D* ≤ 60 (fine sediments)

n = 1 - 0.56log10D*

For D* > 60

n = 0

AAW = 0.17

m = 1.5

CAW= 0.025

The Ackers & White (1993) equation uses revised equations for n, AAW, n and CAW in the Ackers-White (1973) equations given above.

The revised equations are:

 

For 1 < D* ≤ 60 (fine sediments)

For D* > 60; m = 1.78

The Engelund-Hansen (1967) equation was developed by equating the work done by the drag forces of the flow to the potential energy gained by particles as they move up the face of a dune. The form of the equation used is:

 

 

The Westrich-Jurashek (1985) equation was developed from laboratory experiments on the transporting capacity of rigid boundary channels. Only fine sediments were used (0.026 to 0.11 mm) in the experiments, which recorded the maximum transport without deposition on the channel bed. An energy balance equation was fitted to the results.

The form of the equation used is:

 

 

The applicability of the equation is limited to fine sediments and sediment transport over rigid boundaries.

 

 

where:

 

 
 
 

The equations used by the Velikanov model are the same as those used by the 1D water quality model.

See the Conduit Model topic for details.

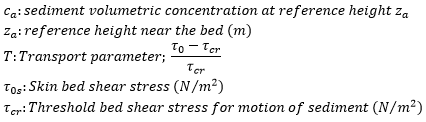
Sediment volumetric concentration ca:

 

 

where:

 

Sediment volumetric concentration ca:

 

 

where:

Skin friction Shields parameter q:

 

Shields parameter qcr:

 

Sediment volumetric concentration ca:

 

 

 

 

 
 

 

 

Shear stress is calculated as density multiplied by the square of the shear or friction velocity.

 

 

Where:

= Shear stress (N/m2)

= Density (kg/m3)

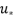= Friction velocity (m/s)

CD= Friction coefficient

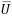= Velocity (m/s)

K = 0.41: von Karman constant

h = Water depth (m)

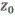: bed roughness length (m).

For rough flow conditions

Note that the only difference between skin friction methods is the definition of the friction coefficient.

In the case of more than one sediment fractions, the combined shear stress result should be the sum of the shear stresses for each sediment fraction.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Parameterisation of Shields curve

 

 

Water Quality and Sediment Parameters