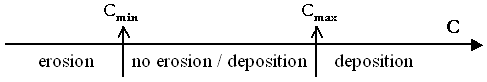Conduit Model
The conduit model is used to calculate the transport of suspended sediment and dissolved pollutant, and the erosion and deposition of sediment, in conduits. The transport process and the sediment erosion and deposition process are solved separately within each time step.
As with the hydraulic conduit model, a conduit is represented as a conceptual link of defined length between two nodes in the network. Control structures are treated as links of zero length in which no erosion or deposition takes place.
It is assumed that:
- The flow is one-dimensional in the conduit.
- The concentration of any suspended sediment and dissolved pollutant is fully mixed across the section of the conduit.
- The suspended sediment and dissolved pollutants are transported along the conduit with the local mean velocity of the flow.
- Dispersion of the suspended sediment and dissolved pollutant along the conduit is negligible.
- Erosion of sediment from the bed is instantaneous
- Deposition of suspended sediment depends on a settling velocity calculation.
- Deposition of suspended sediment does not affect the hydraulic calculations.
Transport
The equation describing the transport of the suspended sediment and the dissolved pollutant is based on conservation of mass. With the assumptions listed above, this leads to the one-dimensional advection equation as described in, for example, Cunge J A et al (1980).
![]()
where
c is the concentration (kg/m3)
u is the flow velocity (m/s) - obtained from the hydraulic simulation
t is time (s)
x is the spatial co-ordinate (m).
The boundary condition at the upstream end required for this equation is generated by the Network Model.
The carrying capacity of the flow is calculated using one of the three erosion/deposition models available in InfoWorks ICM . See Sediment Erosion and Deposition for more details.
Numerical Techniques
Advection
The advection equation is solved in each conduit by the Holly-Preissmann scheme (Holly F.M. & Preissmann A. (1977)). This is a semi-Lagrangian method. It tracks conceptual parcels of pollutant in the flow.
The solution of the advection equation is known to be constant:
![]()
along trajectories, X, given by:
![]()
This differential equation is solved for the trajectories by the mid-point rule:
![]()
with the velocities at the half time level generated by averaging the velocities at the two most recent time levels, and the position of the trajectory at the half time level generated by iteration. This gives a method which is second order in time.
Since the position of the foot of a trajectory at the previous known time level, Xn, does not generally coincide with a computational point, the value at the foot is generated by interpolation. The solution generated by this scheme is unconditionally stable - there is no restriction on the allowable size of the time step.
Cubic interpolation at the foot of a trajectory gives a solution which is third order in space but it can introduce un-physical oscillations to the numerical solution. This is avoided by the use of flux-corrected transport (FCT) (Boris J.P. and Book D.L. (1973)) - the local weighted averaging of two different numerical solutions to impose monotonicity.
The flux-corrected transport solution is not conservative. In the InfoWorks ICMwater quality model, conservation is recovered by the use of sub-optimal weights in the FCT local averaging. See Priestley A. (1993).
1D Diffusion
It is also possible to simulate 1d diffusion, if required. Once the 1D engine has solved advection of the determinants, it can then calculate the diffusion. The equations for 1D diffusion are described in the topic 1D Diffusion.
Sediment Erosion and Deposition
The erosion/deposition model to be used is set in the Water Quality and Sediment Parameters for the network.
The following assumptions and limitations apply to erosion and deposition of sediment:
- suspended sediment is assumed to be well mixed
- erosion of suspended sediment is instantaneous
- deposition is based on settling velocity
- cohesive forces are ignored
- no deposition is allowed to occur if the total sediment depth (active plus passive layer) is greater than a user defined percentage (up to 80%) of pipe depth. See Sediment for more information
InfoWorks ICM supports three different models for calculating erosion and deposition in pipes. These models are:
The Ackers White algorithm is based on the Ackers-White theory (Ackers P. (1991)).
- At each computational point along each pipe, a non-dimensional carrying
capacity, Cn is calculated that represents
the maximum concentration of a given sediment fraction that can be held
within the flow. The equation used to calculate Cnis:
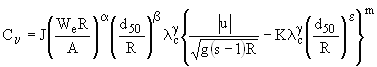
(1)
where
lc is the composite friction factor which is calculated using the Colebrook-White formula (as described in Ackers J.C. et al (1994))
R is the hydraulic radius (=A/Po) (m)
Po is the wetted perimeter (m)
We is the effective bed width (m)
A is the cross sectional area of the flow (m2)
U is the local flow velocity (m/s)
The remaining parameters are all functions of the dimensionless grain size:
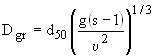
(2)
where
n is the kinematic viscosity of water (m2/s)
g is the acceleration due to gravity (m/s2)
s is the specific gravity of the sediment fraction
d50 is the average sediment particle size (m)
- The non-dimensional carrying capacity number is converted to a maximum
concentration by
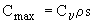
(3)
- If the actual concentration is greater than Cmax then the excess sediment is deposited. If the actual concentration is less than Cmax the bed is eroded until either Cmax = Cactual or all the bed has been eroded. Erosion is assumed to occur instantaneously while the rate of deposition is a function of the sediment settling velocity.
- All flow concentrations and bed masses are updated before the sediment is advected at the next timestep.
The Velikanov model is one of the algorithms available for calculating the erosion and deposition of sediment in pipes. The model was applied in this way based on research done by Anjou Recherche in France. Anjou Recherche is the main water operations research centre for Vivendi Water.
The Velikanov model determines two concentrations (Cminand Cmax). If the flow concentration is below Cmin then erosion occurs to achieve Cmin if possible. If the flow concentration is above Cmax then deposition occurs to achieve Cmax if possible. If the flow concentration is between Cminand Cmax then no erosion or deposition occurs.
|
|
|
|
|
|
The algorithm is described in Zug M. et al (1998). You are referred to this paper for full details of the model.
The KUL model was developed at the Katholieke Universiteit Leuven in Belgium and is described in Bouteligier R. et al (2002).
The KUL model determines two shear critical stress values (tau critical deposition and tau critical erosion). If the shear stress is below tau critical deposition then deposition occurs. If the shear stress is above tau critical erosion then erosion occurs. If the shear stress is between tau critical deposition and tau critical erosion then no erosion or deposition occurs. The rate of deposition or erosion depends on the shear stress.
Dependent Sediment Fractions
Multiple sediment fractions can be modelled independently or dependently. If multiple sediment fractions are modelled independently then the above algorithm is used for each sediment fraction. If the sediment fractions are modelled dependently then the following algorithm is used at the end of each water quality timestep.
- Calculate the total load in the flow

- Calculate single representative d50 and s for the fractions in the flow as a weighted average based on the concentration
of the fractions present in the flow
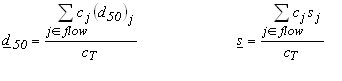
- Calculate the flow capacity for the representative fraction using the carrying capacity equation above.
- If cT > rsc*n (flow capacity is exceeded) then deposition occurs,
and the excess is spread between the fractions in the flow
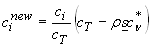
- If cT < rsc*n (there is available flow capacity) then erosion
occurs, and the available capacity is spread between the fractions on
the bed
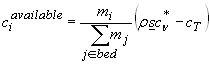
 Water Quality
Water Quality