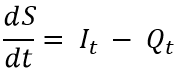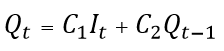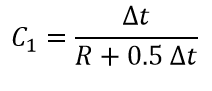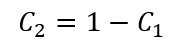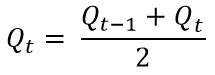Clark Model
The Clark routing model uses the Clark unit hydrograph method. An outline of this method, which has been extracted from the Innovyze H2OMAP SWMM User's Guide, is described below.
Clark’s method derives a unit hydrograph by explicitly representing the processes of translation and attenuation, which are the two critical phenomena in transformation of excess rainfall to runoff hydrograph. Translation refers to the movement, without storage, of runoff from its origin to the watershed outlet in response to gravity force, where as attenuation represents the reduction of runoff magnitude due to resistances arising from frictional forces and storage effects of soil, channel, and land surfaces.
Clark (1945)[1] noted that the translation of flow through the watershed could be described by a time-area curve (see Figure 1), which expresses the curve of the fraction of watershed area contributing runoff to the watershed outlet as a function of travel time since the start of effective precipitation. Each sub-area is delineated so that all the precipitation falling on the sub-area instantaneously has the same time of travel to the outflow point. Developing a time-area curve for a watershed could be a time consuming process. For watersheds that lack derived time-area diagram, the HEC-HMS model[2], which was developed at the Hydrologic Engineering Center (HEC) of the U.S. Army Corps of Engineers, uses the following relationship (HEC, 2000):
Where: Ac,t is cumulative watershed area contributing at time t AT is total watershed area tc is time of concentration of the watershed |
If the incremental areas, denoted as Ai in Figure 1, are multiplied by a unit depth of excess rainfall and divided by Δt, the computational time step, the result is a translated hydrograph that is considered as an inflow to a conceptual linear reservoir located at the watershed outlet.

Figure 1
To account for storage effects, the attenuation process is modelled by routing the translated hydrograph through a linear reservoir with storage properties similar to those of the watershed. The routing model is based on the mass balance equation:
Where: dS/dt is time rate of change of water in storage at time t It is average inflow, obtained from the time-area curve, to storage at time t Qt is outflow from storage at time t |
For linear reservoir model, storage is related to outflow as:
Where: R is a constant linear reservoir parameter that represents the storage effect of the watershed. Usually, lag time (tL) is used as an approximation to R. |
Combining and solving Equations 2 and 3 using a finite difference approximation provides:
Where: C 1 and C 2 are routing coefficients calculated as:
|
The average outflow during period t is:
|
If the inflow, It, ordinates are runoff from a unit depth of excess rainfall, the average outflows derived by Equation 7 represent Clark’s unit hydrograph ordinates. Clark’s unit hydrograph is, therefore, obtained by routing a unit depth of direct runoff to the channel in proportion to the time-area curve and routing the runoff entering the channel through a linear reservoir.
Note that solution of Equations 4 and 7 is a recursive process. As such, average outflow ordinates of the unit hydrograph will theoretically continue for an infinite duration. Therefore, it is customary to truncate the recession limb of the unit hydrograph where the outflow volume exceeds 0.995 inches or mm.
Clark’s method is based on the premise that duration of the rainfall excess is infinitesimally small. Because of this, Clark’s unit hydrograph is referred to as an instantaneous unit hydrograph or IUH. In practical applications, it is usually necessary to alter the IUH into a unit hydrograph of specific duration. This can be accomplished by lagging the IUH by the desired duration and averaging the ordinates.
References
[1] Clark, C. O., 1945. Storage and the unit hydrograph. Transactions, ASCE, Vol. 110, Paper No. 2261, 1419-1446
[2] HEC-HMS Technical Reference Manual. March 2000. US Army corps of Engineers, Hydrologic Engineering Centre, USA