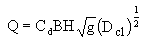Sluice Gates
Sluice gates or penstocks may be used as the outflow control on storage tanks or ponds. InfoWorks ICM includes two types of sluice: radial gate and vertical gate. The gate can be set to a fixed opening or adjusted during the analysis to represent manual or automatic operation of the gate.
A sluice gate is represented as a link of zero length, forming a head-discharge relationship between two nodes. The boundary conditions between the link and a node are that of equal water levels. The sluice gate invert level determines when the control first comes into operation. The flow characteristics are identical in both the positive and negative directions.
Flow Characteristics
InfoWorks ICM uses the same flow equations for vertical and radial sluice gates, but in the case of a radial sluice gate, angles are used to specify the geometry and operation of the gate.
In the case of the upstream depth being less than the opening height InfoWorks determines the flow using the thin plate rectangular weir model.
In the case of a submerged sluice gate upstream, InfoWorks calculates flow as the lower of the flow values determined using the weir equation and the orifice equations described below.
Orifice equations
Assuming a submerged sluice gate upstream the governing model equation depends upon the flow conditions under the sluice gate and the downstream water level (see Henderson, 1966 and Chow, 1959). If the flow under the sluice gate is supercritical and the downstream depth is less than the conjugate depth to the gate opening or the flow under the sluice gate is subcritical and operating under free discharge conditions then the governing equation is:
|
|
where Dcl - height of water level above the centroid of the orifice (m) |
This is modified under drowned conditions by:
|
|
where Q - discharge (m3/s) Cd - discharge coefficient B - penstock breadth (m) H - penstock opening height (m) g - acceleration due to gravity (m/s2) Du - upstream depth above invert (m) Dd - downstream depth above invert (m) |
Weir equations
If the upstream depth being less than the opening height the simulation engine determines the flow using the thin plate rectangular weir model.
|
|
when Dd is less than zero (free flow), or
when Dd is greater than or equal to zero (drowned flow) where: Q - discharge (m3/s) Cd2 - secondary discharge coefficient B - penstock breadth (sluice width) (m) g - acceleration due to gravity (m/s2) Du - upstream depth above invert (m) Dd - downstream depth above invert (m) |
Villemonte Equation
If the Use Villemonte equation has been chosen as a Simulation Parameter, when the sluice is under drowned weir flow conditions, the Villemonte formula is used to modify the free discharge:
|
|
where: Q is the discharge Q0is the free discharge Du is the upstream depth with respect to the invert Dd is the downstream depth with respect to the invert |