Simulation Parameters

Min base flow depth

This is the minimum absolute baseflow depth that will be used for base flows in conduits.

Valid values: 0 < Minimum base flow depth << Minimum conduit height.

This Base Flow used for calculation purposes should not be confused with the Subcatchment Base Flow, which is a real inflow into the system.

min_base_flow_depth

Double

Y

3

0.02 m

0.001

99

Base flow factor

Base flow is necessary to ensure numerical stability of the St. Venant equations. By default the base flow applied is equal to 5% of the conduit height (Base Flow Factor of 0.05) (10% for steeper pipes.)

The simulation engine adds base flow to maintain numerical stability at low depths. It does this by altering the true upstream (higher) boundary condition so that there is effectively a wall of the base flow depth at the upstream end of the conduit. The simulation engine then adds the normal flow for the base flow depth to the flows in the conduit.

At the true downstream end of the conduit, the boundary condition uses the true flow, so that in effect the base flow is lost between the conduit end and the connected node. This means that node volume balance calculations are based on the true flows.

• The simulation engine reports flows net of base flow

• Velocities are calculated as net flow / area. For low depths you may find that the simulation engine underestimates velocities compared to flow survey results.

The base flow factor is used to determine the base flow depth in conduits using the following equation:

Valid values: 0 < Base Flow Factor << 1.

base_flow_factor

Double

3

.05

0

1

Slope where base flow is doubled

This is the slope above which the base flow factor is doubled when determining the base flow depth.

Valid values: 0 £  Slope where base flow is doubled

slope_base_flow_x2

Double

S

4

.01 m/m

0

1

Min space step

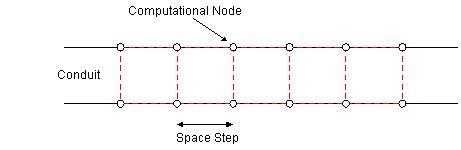
The Space Step parameters determine the number of computational nodes per conduit / river reach.

The Space Step is the distance between computational nodes along the conduit / river reach. Valid values are:

Minimum Space Step (DXMIN): DXMIN > 0, DXMIN < DXMAX

Maximum Space Step (DXMAX): DXMAX > 0, DXMAX > DXMIN

In addition, for river reaches:

• DXMAX should not be greater than 1/(2S), where S is the river slope
• DXMAX should not be greater than 0.2D/S, where D is the typical depth of flow

The Space Step is determined by the Conduit width multiplier:

Minimum Number of Computational Nodes is the global minimum number of computational nodes per conduit. Controls always have 2 computational nodes. The software will allocate at least 5 computational nodes per conduit. If the number of computational nodes determined by the other space step parameters exceeds the minimum, the software will use that number instead.

min_space_step

Double

L

2

.5 m

0.01

9999

Max space step

See Min space step

max_space_step

Double

L

2

100 m

0.01

9999

Conduit width multiplier

See Min space step

width_multiplier

Double

2

20

0

999

Min number of computational nodes

See Min space step

min_computational_nodes

0

5

5

99999999

Min slot width

Minimum width of the Preissmann slot (overrides value determined by Celerity ratio).

Valid values: 0 < Min slot width << Minimum conduit width.

min_slot_width

Double

L

5

0.001 m

0.00001

99

Celerity ratio

The Preissmann slot is used in the hydraulic simulation to model pressurised flow in closed conduits.

The Celerity ratio determines the width of the Preissmann slot used in the software to model surcharged flow. The slot width is such that the celerity in the slot is Celerity ratio x the celerity at half conduit height. The standard ratio was chosen so that surcharged flows could be modelled robustly and accurately. This results in a slot that is 2% of the width of the conduit (slightly different for some conduit shapes). If the software is being used to model storage in large surcharged trunk sewers you may want to reduce the slot width to reduce the additional storage that it generates (note that the slot transition generally adds 4-5% area depending on shape). To do this, increase the value of Celerity ratio - a value of 14.414 produces a slot that is 1% of conduit width. Note that narrower slots may make the model less stable. The slot width is inversely proportional to Celerity ratio.

Valid values: Celerity ratio > 0

The equations used to calculate the slot width are as follows:

celerity_ratio

Double

2

10

0

9999

Lower Froude number

This is the characteristic Froude number above which the inertia terms in the Saint-Venant equations are phased out for a conduit. The characteristic Froude number for a conduit is determined at half depth.

Valid values: 0 < Lower Froude number < Upper Froude number

lower_froude_number

Double

3

.8

0

99

Upper Froude number

This is the characteristic Froude number above which the inertia terms in the Saint-Venant equations are dropped. Note that using a value above 1.0 may result in instabilities during simulation. The conduits with the inertia terms dropped will be solved faster by the hydraulic simulation.

Valid values: Upper Froude number > 0, Upper Froude number > Lower Froude number

upper_froude_number

Double

3

1

0

99

Start timestep (s)

The Initialisation Parameters are used if an initial simulation has not been included in the Simulation State section of the Schedule Hydraulic Run Dialog. The hydraulic system is initialised in a steady state.

• The Start timestep is the initial timestep during the initialisation process.

• The Max timestep is the maximum allowed timestep during the initialisation process.

• The Phase-in time is the time over which the boundary conditions (initial inflows and tide levels) are linearly phased in during initialisation.

The simulation engine will perform up to five initialisation phases. Each time initialisation fails, the phase-in time will be multiplied by a factor of 10 and restartedf from the initial (dry) condition.

start_timestep

Double

2

7.5

0.01

9999

Max timestep (s)

Maximum allowed timestep during initialisation process.

See Start timestep

max_timestep

Double

2

1920

0.01

9999

Phase-in time (min)

Time over which the boundary conditions (initial inflows and tide levels) are linearly phased in during initialisation.

See Start timestep

phase_in_time

Double

2

15

0.01

99999

Steady state flow tolerance

See Start timestep

steady_tol_flow

Double

Q

6

.0005 m3/s

0.000001

999

Steady state depth tolerance

See Start timestep

steady_tol_depth

Double

Y

6

.005 m

0.000001

999

Max number of timestep halvings - initialisation

Maximum number of timestep halvings to allow convergence of the Newton-Raphson method during the initialisation process.

ini_max_halvings

0

10

1

30

Max number of iterations - initialisation

Maximum number of iterations per timestep during the initialisation process.

ini_max_iterations

0

10

1

999

Max number of iterations after doubling - initialisation

Maximum number of iterations allowed after the timestep has been doubled during the initialisation process. (Rapid convergence of the Newton-Raphson method may result in the timestep being doubled).

ini_max_iterations_x2

0

7

1

999

Tolerance for flow

During the initialisation process, convergence is achieved when:

ini_tolerance_flow

Double

4

.01

0.0001

9

Flow tolerance scaling factor - initialisation

See Tolerance for flow - initialisation

ini_scaling_flow

Double

3

1

0.001

999

Tolerance for depth

See Tolerance for flow - initialisation

ini_tolerance_depth

Double

4

.01

0.0001

9

Depth tolerance scaling factor - initialisation

See Tolerance for flow - initialisation

ini_scaling_depth

Double

3

1

0.001

999

Tolerance for level

See Tolerance for flow - initialisation

ini_tolerance_level

Double

4

.01

0.0001

9

Level tolerance scaling factor - initialisation

See Tolerance for flow - initialisation

ini_scaling_level

Double

3

1

0.001

999

Min depth in conduits - initialisation

Minimum depth imposed by the simulation engine during the initialisation process.

ini_min_depth

Double

Y

5

.01 m

0.00001

9

Min plan area at nodes - initialisation

Minimum node plan area imposed by the simulation engine during the initialisation process.

ini_min_node_area

Double

NA

3

1 m2

0

9999

Time weighting factor

q is used in the Preissmann 4-point scheme.

The 4-point scheme is only unconditionally stable when q > 0.5. The value of q = 1.0 provides maximum numerical dispersion during initialisation.

ini_time_weighting

Double

3

1

0

1

0.5

Tolerance for volume balance

If Tolerance for volume balance is set to 0.0 (default), no volume balance checking will be carried out.

To enable volume balance checking, define a value greater than zero. The recommended value to use is 0.01. When volume balance checking is enabled the simulation engine checks the volume balance at each node at each iteration where the flow, depth, and level increments are within tolerance.

If volume balance / (volume balance scaling factor + |largest volume in/out/change in storage|) is greater than the Tolerance for volume balance then the engine will do another iteration, unless the engine has already done the maximum number of iterations for this timestep, in which case the engine will halve the timestep.

ini_tolerance_volbal

Double

4

0

0

9

Volume balance tolerance scaling factor - initialisation

See Tolerance for volume balance (Initialisation)

ini_scaling_volbal

Double

3

1

0

999

Relax tolerance from run t/s - initialisation

During the initialisation phase:

• When this option is checked, if the current timestep is less than the run timestep, the simulation will relax tolerances using a factor based on the run timestep.

• When this option is unchecked, the simulation will relax tolerances if the current timestep is less than 60s, using a factor based on a timestep of 60s.

It is strongly recommended that this option is checked for networks that contain 2D Zones.

ini_relax_tol

Boolean

0

True

Max number of timestep halvings - simulation

Maximum number of timestep halvings to allow convergence of the Newton-Raphson method during the simulation.

sim_max_halvings

0

10

1

30

Max number of iterations - simulation

Maximum number of iterations allowed per timestep.

sim_max_iterations

0

10

1

999

Max number of iterations after doubling - simulation

Maximum number of iterations allowed after the timestep has been doubled. (Rapid convergence of the Newton-Raphson method may result in the timestep being doubled).

sim_max_iterations_x2

0

7

1

999

Tolerance for flow - simulation

During the simulation, convergence is achieved when:

sim_tolerance_flow

Double

4

.01

0.0001

9

Flow tolerance scaling factor - simulation

See Tolerance for flow - simulation

sim_scaling_flow

Double

3

1

0.001

999

Tolerance for depth - simulation

See Tolerance for flow - simulation

sim_tolerance_depth

Double

4

.01

0.0001

9

Depth tolerance scaling factor - simulation

See Tolerance for flow - simulation

sim_scaling_depth

Double

3

1

0.001

999

Tolerance for level - simulation

See Tolerance for flow - simulation

sim_tolerance_level

Double

4

.01

0.0001

9

Level tolerance scaling factor - simulation

See Tolerance for flow - simulation

sim_scaling_level

Double

3

1

0.001

999

Min depth in conduits - simulation

Minimum depth imposed by the simulation engine

sim_min_depth

Double

Y

5

.01 m

0.00001

9

Min plan area at nodes - simulation

Minimum node plan area imposed by the simulation engine

sim_min_node_area

Double

NA

3

1 m2

0

9999

Time weighting factor - simulation

q is used in the Preissmann 4-point scheme.

The 4-point scheme is only unconditionally stable when q > 0.5; the value of q = 0.65 used during simulation introduces a small degree of numerical dispersion.

sim_time_weighting

Double

3

.65

0

1

0.5

Tolerance for volume balance - simulation

If Tolerance for volume balance is set to 0.0, no volume balance checking will be carried out.

To enable volume balance checking, define a value greater than zero. The recommended value to use is 0.01. When volume balance checking is enabled the simulation engine checks the volume balance at each node at each iteration where the flow, depth, and level increments are within tolerance.

If volume balance / (volume balance scaling factor + |largest volume in/out/change in storage|) is greater than the Tolerance for Volume Balance then the engine will do another iteration, unless the engine has already done the maximum number of iterations for this timestep, in which case the engine will halve the timestep.

sim_tolerance_volbal

Double

4

0.01

0

9

Volume balance tolerance scaling factor

See Tolerance for volume balance - simulation

sim_scaling_volbal

Double

3

1

0

999

Relax tolerance from run t/s - simulation

During the simulation phase:

• When this option is checked, if the current timestep is less than the run timestep, the simulation will relax tolerances using a factor based on the run timestep.

• When this option is unchecked, the simulation will relax tolerances if the current timestep is less than 60s, using a factor based on a timestep of 60s.

It is strongly recommended that this option is checked for networks that contain 2D Zones.

sim_relax_tol

Boolean

0

True

A check in the box (default) indicates that SWMM5 RDII (Rainfall Derived Infiltration and Inflow) is to be used in the simulation. If unchecked, the pre-SWMM 5 RDII implementation will be used in the simulation.

Note

Pre-SWMM 5 RDII does not support the monthly variation and initial abstraction functionality that is available in SWMM5 RDII for Monthly RTK Hydrographs, but does allow multiple subcatchments that use RTK Hydrographs (not necessarily the same one) to drain to a single node.

Stay pressurised

A pipe should only be pressurised if it is to stay pressurised throughout the simulation. However it is very common that people model pressurised pipes that are not in fact pressurised. By default, the simulation engine will switch to the full solution model for the rest of the simulation if a pressure pipe is not surcharged.

You may want to check the Stay pressurised option if you have, for example, a rising main that numerically temporarily goes out of surcharge because of water hammer effects when a pump switches on or off. The simulation may fail in this case, if you have inappropriately set a conduit as a pressure pipe. You should only use the pressurised pipe model for conduits that you know remain permanently surcharged.

The field settings are:

• unchecked - simulation engine will switch to the full solution model for the rest of the simulation if a pressure pipe is not surcharged

• checked - the simulation engine only switches a pressure pipe to the full solution model if it is not surcharged at the end of initialisation. If during the simulation the pipe becomes unsurcharged, the engine will continue to use the pressurised pipe model

stay_pressurised

Boolean

0

False

Don't linearise conveyance

In culverts, the conveyance is greater just before the culvert becomes full than at the point when the culvert becomes surcharged. This effect is most pronounced in wide rectangular culverts, and occurs due to the effect of the roughness of the roof of the culvert.

When this is option is unchecked (default), conveyance tables are linearised to the pipe full value to eliminate turning points in the conveyance function used by the solver. This is shown by the red line on the graph below. This results in the underestimation of flow capacity in rectangular culverts. However, it is more stable mathematically.

When this option is checked, the simulation engine does not linearise conveyance tables (see the black line on the graph). Using this option may result in instabilities when the conduit enters/leaves surcharge.

Conduit Conveyance

dont_linearise_k

Boolean

0

False

No. of geometry table entries

This field determines the number of entries the simulation uses for conduit cross-section geometry lookup tables between the invert and soffit. More entries provide a more accurate representation of the geometry, at the expense of memory use and computational effort.

You may need to change this parameter to get a more accurate representation of pipe behaviour close to pipe full when you turn on the Don't linearise conveyance option above.

geometry_table_entries

0

15

15

999

Use full area for headloss calculations

By default the checkbox is unchecked. The value of velocity passed through to the headloss calculations is calculated from:

When this option is checked headloss calculations are carried out using the full cross section area of the pipe.

use_full_area_for_hl

Boolean

0

False

Inflow is lateral

The value of this field affects the way in which the simulation engine handles inflow as defined in the Inflow field of conduit, river reach, channel and bridge links. For new models, Innovyze recommend that this field is checked. However, if you want to reproduce the behaviour of the simulation engine prior to InfoWorks ICM, version 6.5 then do not check this field.

• If this field is checked, the engine applies these flows laterally to links.
• If this field is not checked, the engine applies these flows to the node at the end of the link with the highest invert level. In the case of equal invert levels, the flow is assigned to the upstream node.

inflow_is_lateral

Boolean

0

False

Bottom of headloss transition

The Bottom of headloss transition and Top of headloss transition parameters are used to define a transition zone in which headloss in conduits is phased out, with the purpose of eliminating unrealistically high headloss results for links with flows at low depths.

• Below the bottom of the transition zone, headloss is zero

• Above the top of the transition zone, headloss is calculated as normal

• Within the transition zone, headloss is linearly phased out

The values are given as a proportion of conduit height minus sediment depth:

hl_trans_bottom

Double

3

0

0

1

Top of headloss transition

Used to define a transition zone in which headloss in conduits is phased out, with the purpose of eliminating unrealistically high headloss results for links with flows at low depths.

See Bottom of headloss transition for further details.

hl_trans_top

Double

3

0

0

1

Use Villemonte equation

When this field is checked the simulation will use the Villemonte equation for drowned weir flow.

use_villemonte

Boolean

0

False

Drop inertia in pressure pipes

Check this parameter to exclude modelling of inertia in pressure pipes.

See Pressurised Pipe Model for more information.

pressure_drop_inertia

Boolean

0

True

When calculating bank flow for a drowned spill segment, linearised flow equations will be used when the head difference at both ends of the segment is below this threshold.

Applicable to lateral banks, inline banks and irregular weirs; this parameter is used to avoid oscillating flows as the head difference over the bank approaches zero.

If set to null, a value of zero is assumed (no linearisation).

Check this parameter to make groundwater infiltration depend on the depth in the groundwater destination node.

In existing networks (created before Version 8.0) this option will be unchecked. In new networks this option will be checked.

The simulation engines uses the equivalent roughness concept to provide a roughness value for a wetted perimeter that has more than one roughness value.

This parameter allows you to choose whether the perimeter is weighted using n (N) or 1/n (MANNING) to represent roughness.

Check this parameter to weight Manning roughness by n. If unchecked (default), Manning roughness will be weighted by 1/n.

Used as a measure to avoid oscillating flows due to ground level discrepancy between manholes and 2D mesh elements.

Check this parameter to use the elevation in 2D zones to set the elevation at 1D nodes connected to the 2D zone.

If this option is unchecked, the engine will use the depth in 2D zones to set the depth above ground at 1D nodes.

See Defining 2D Nodes for more information.

Note

This setting is over-ridden by the setting on the 1D-2D linkage basisfield for individual nodes. See Node Data Fields for further information.

Check this parameter to use the net inflow into an element when calculating maximum flow that can be exchanged between the 2D element and a 1D node within the element. This method monitors the error between the head in the element (measured head) and the corresponding head given by the net inflow into the element (equilibrium head). A PID controller is used to minimise the error by adjusting the maximum flow that can be exchanged between the 2D and 1D network.

If this option is unchecked, the engine will use the volume in the element to calculate the maximum flow that can be exchanged. This method may result in discrepancies between head in the 2D mesh and inflow to the 1D network, particularly in cases where 1D nodes are located within small elements and when using long timesteps.