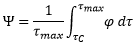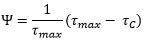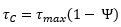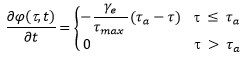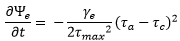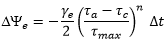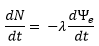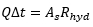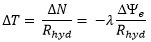Water quality - turbidity analysis
Turbidity analysis can be used as a tool to predict discolouration events. The results from the analysis can be used to design flushing strategies with the aim of improving water quality in the network and reducing customer complaints.
To include Turbidity Analysis in a Water Quality Simulation, check the Do Turbidity Analysis option in the Water Quality Options dialog when scheduling a run.
For details on the model parameters required for Turbidity Analysis, see the Water Quality Parameters topic.
Additional results will be available when a Turbidity Analysis is run:
- Turbidity: the turbidity at the node
- Stored Turbidity Ratio: the ratio of the amount of discolouration material to the total amount of such material bound to the pipe wall in this pipe
- Peak Turbidity: the peak value of the turbidity in all segments in this pipe at the completion of the water quality time loop
Technical details
The InfoWorks WS Turbidity Analysis model uses an adaptation of the approach to modelling erosion and regeneration of discolouration material in water supply systems published by Furnass et al (2014).
In Furnass et al (2014), the amount of discolouration material bound to the pipe wall is represented by a material condition function φ(t, t), effectively a shear stress distribution function, defined as the relative amount of discolouration material bound to the pipe wall for a given shear stress, t.
This approach has been influenced more by the regeneration than the erosion process, however the implementation in InfoWorks WS models the erosion process only, as regeneration occurs over a long time-frame of typically months or years.
In Furnass et al (2014), it is the regeneration process that requires the full shear stress distribution function but it is useful to keep this as a starting point.
With erosion we are free to integrate φ over a suitable range of t. If the lowest value of t for which φ is non-zero is denoted tC, effectively the corrosion layer shear strength, then this can be rewritten:
|
|
|
where Ψ can be identified as the stored turbidity volume ratio. If, at least initially, φ only takes the values of 0 or 1, and equals 1 over the whole integral range, this can be rewritten:
|
|
|
Thus the equation for the corrosion layer shear strength versus stored turbidity volume ratio is:
|
|
|
Only two parameters are required as input, tmax, the maximum shear strength, and an initial value for tC, the initial shear strength.
In a modification of the Furnass et al (2014) paper, erosion is denoted by:
|
|
where: ta is the applied shear stress at the wall at time t. |
If this is integrated over t from tC to ta we obtain:
|
|
|
For InfoWorks WS this has been rewritten:
|
|
|
with the exponent 2 generalised to n. The parameter ge, the erosion coefficient, has units of s-1 and, along with a value for n, the erosion exponent, is required as input.
Furnass et al (2014) gives an expression for the material release rate from a unit area of pipe wall which, after integration over t, has been rewritten:
|
|
|
The release coefficient λ has units NTU.m and is required as input.
The change in turbidity DT due to erosion in the time Dt is therefore obtained by multiplying by the area swept out, As, and dividing by the volume the material is released into, QΔt, or, using:
|
|
|
we obtain:
|
|
|