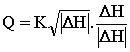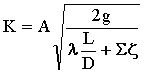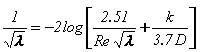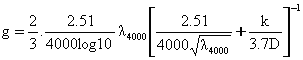Pipe calculation information
For modelling purposes, InfoWorks WS Pro sub-divides links into the following. A pipe is represented in the model by:
- two terminal nodes ("i" and "j")
- length, L (m)
- internal diameter, D (mm)
- friction coefficient,l
- sum of local head-loss coefficients, z
The friction coefficient is used to calculate the headloss along a pipe. In the InfoWorks simulation engine, headloss is always calculated using the Darcy Weisbach formula.
where:
and: Q > 0 if Hj > Hi Q is negative if Hj < Hi |
For the "node-oriented" method this equation is often written as:
where:
|
K is a measure of capacity of the pipe. K depends upon the value of Reynolds number Re.
where:
|
You can enter a friction coefficient in the format for one of three friction formulae:
- Darcy Weisbach
- Hazen Williams
- Colebrook White
InfoWorks then converts the friction coefficient using methods described below.
Darcy Weisbach
The parameter l entered by the user is used directly. lis non-dimensional.
Hazen Williams
The Hazen Williams friction formula:
where: m = 4.8704 n = 1.852 C is the friction coefficient |
InfoWorks uses the following relationship to convert C to the Darcy Weisbach friction coefficient l:
|
The equivalent Darcy-Weisbach factor is dependent on the Reynolds number for flow in each pipe and is re-evaluated at each iteration of the simulation.

If the Use dynamic friction factors option is not selected in the Simulation Options dialog, InfoWorks converts the Hazen Williams coefficient C to a Darcy-Weisbach friction coefficient only once for each pipe, assuming a flow speed of 1 m/s.
Colebrook White
The user may decide to specify Colebrook White internal roughness k.
The equivalent Darcy-Weisbach friction factor, l, is modelled on the Moody diagram, is dependent on the Reynolds number (Re) for flow in each pipe and is re-evaluated at each iteration of the simulation.

If the Use dynamic friction factors option is not selected in the Simulation Options dialog, InfoWorks converts the Hazen Williams coefficient C to a Darcy-Weisbach friction coefficient only once for each pipe, assuming a flow speed of 1 m/s.
For Re >= 4000, InfoWorks solves the Colebrook-White equation iteratively to convert the specified internal roughness k to the Darcy-Weisbach friction coefficient to an accuracy of 0.1%:
|
For Re < 4000 there are two methods for modelling the Moody diagram in the critical zone between laminar flow and the transition / turbulent zone.
- Cubic spline interpolation
- Modified CW-Moody (constant value)
The Modified CW-Moody method is the most stable numerically and for this reason is set as the default method in the Simulation Options dialog. Although this option may over-estimate the friction factor, this generally only occurs for low pipe flows and any hydraulic effects are not likely to be significant.
Cubic Spline Interpolation
For 2000 < Re < 4000, a cubic polynomial interpolation using standard cubic spline methods to match the laminar friction factor at Re = 2000, the Colebrook-White derived value at Re = 4000(l4000) and their respective gradients:
where:
|
For Re <= 2000, the friction factor is calculated from the Hagen-Poiseuille formula for laminar flow:
|
Modified CW-Moody (constant value):
For 2000 < Re < 4000, a constant value is imposed equal to the friction factor calculated from the Colebrook-White equation at a Reynolds number of 4000:
|
For Re <= 2000, the friction factor is the maximum of the Hagen-Poiseuille formula for laminar flow and the constant value above with a maximum cut-off value of 8 for Re<= 8.
|