Blockages

A blockage can be used to model a time-varying obstruction with user-defined contraction and expansion loss coefficients. The blockage is assumed to be vertical; in other words, the same proportion of the flow area is obstructed whatever the water level.

The blockage can be used in a channel, conduit or river reach, or it can be associated with a bridge opening.

Blockage data fields are used to define a general blockage associated with a channel, conduit or river reach while a blockage associated with a bridge opening is defined using the Bridge Blockage data fields.

There are five types of general blockage:

• Local. To model a local obstruction, the blockage should be connected between two identical conduits, channel or river sections. The loss coefficients for contraction and expansion should be set to standard values or used as calibration numbers. They work additively, so setting the Inlet Loss Coefficient to 1.0 and the Outlet Loss Coefficient to 0.5 should give very similar results to setting the Inlet Loss Coefficient to 1.5 and the Outlet Loss Coefficient to 0.0.
• Entry. To model an obstruction at an entry, there must be a single closed conduit downstream of the blockage A closed conduit has a shape that is closed. A conduit with any of the following shapes must not be specified: open rectangle (OREC), open U (OU), open broad egg (OEGB), open narrow egg (OEGN), open trapezoidal (OTn:m, where n, m are integers), or User-defined with non-zero width at the soffit, or asymmetric shapes with non-equal left-hand side/right hand side values for height 1.0

  The Outlet Loss Coefficient will have very little effect on results unless the Blockage proportion is greater than zero (p ≠ 0).

• Exit. To model an obstruction at an exit , there must be a single closed conduit upstream of the blockage A closed conduit has a shape that is closed. A conduit with any of the following shapes must not be specified: open rectangle (OREC), open U (OU), open broad egg (OEGB), open narrow egg (OEGN), open trapezoidal (OTn:m, where n, m are integers), or User-defined with non-zero width at the soffit, or asymmetric shapes with non-equal left-hand side/right hand side values for height 1.0

  The Inlet Loss Coefficient will have no effect unless the Blockage proportion is greater than zero (p ≠ 0).

• Contraction. To model a sudden contraction in an open channel, conduit or a river reach, the blockage should be connected between a upstream section (large) and a downstream section (small). The Outlet Loss Coefficient will have very little effect on results unless the Blockage proportion is greater than zero (p ≠ 0).
• Expansion. To model a sudden expansion in an open channel or conduit or a river reach, the blockage should be connected between an upstream section (small) and a downstream section (large). The Inlet Loss Coefficient will have no effect unless the Blockage proportion is greater than zero (p ≠ 0)

A blockage in a bridge opening can be modelled at the inlet or the outlet or both. However, you cannot model a blockage in a bridge opening at the same time as modelling loss conditions at its inlet and/or outlet.

When modelling general blockages or bridge blockages, the initial blockage is specified as a simple proportion between zero and one. Setting the proportion to one will result in no flow. The rate at which the blockage proportion goes from one state to another is determined by the Positive blocking rate or Negative blocking rate fields. For example, if negative blockage rate is 0.01 /s then it will take 100 s for the blockage proportion to reduce by 1.0.

For reverse flow, the Inlet Loss Coefficient is used for losses on entry and Outlet Loss Coefficient for losses on exit.

Blockage equations

The blockage loss is calculated using the continuity equation:

q1 - q2 = 0

and the Bernoulli equation representing both a contraction and an expansion:

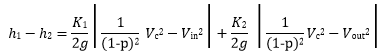
Where:

q1 = Flow at upstream section (m3/s)

q2 = Flow at downstream section (m3/s)

h1 = Stage at upstream section (m AD)

h2 = Stage at downstream section (m AD)

K1 = Inlet loss coefficient

K2 = Outlet loss coefficient

p = Blockage proportion

Vin = Velocity at the upstream section, at a water level h1 and a discharge q1 (m/s)

Vout = Velocity at the downstream section, at a water level h1 and a discharge q1(m/s)

Vc = Velocity at the constriction section* to be obstructed, at a water level h1 and a discharge q1 (m/s)

*For local, entry, & contraction blockage types, the constriction section is the downstream section. For exit, & expansion blockage types, the constriction section is the upstream section.

For bridges, all the velocities (Vin, Vout and Vc) are measured in the bridge opening.

Blockage Results

For details of results fields for all link types, see the Link Results Data Fields topic.