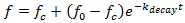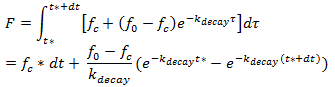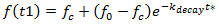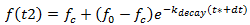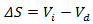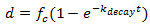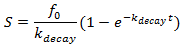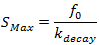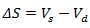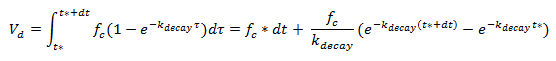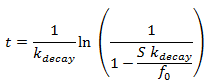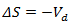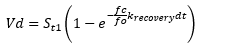2D Infiltration Model

The effective infiltration rate is calculated as described below.

The maximum theoretical infiltration IMAX is given by the function of the infiltration loss coefficient:

IMAX = ILC * Dt (1) where: IMAX = maximum theoretical infiltration (mm) ILC = infiltration loss coefficient Dt = timestep (hr)

If the available water volume in the surface is higher than the maximum infiltration, the soil will be saturated and the effective infiltration will be given by:

IE = ILC + (1 - fixed runoff coeff) * i (2) where: IE = effective infiltration (mm/hr) ILC = infiltration loss coefficient i - rainfall intensity (mm/hr)

If the available water volume in the surface is lower than the maximum infiltration, the effective infiltration will be given by:

IE = AWV / Dt (3) where: IE = effective infiltration (mm/hr) AWV = available water volume Dt = timestep (hr)

A fixed percentage of the net rainfall which becomes runoff is defined.

The effective infiltration rate is calculated using the following:

IE = (1-fixed runoff coeff) * i (1) where: IE = effective infiltration (mm/hr) i - rainfall intensity (mm/hr)

Infiltration either on pervious surfaces or on semi-pervious surfaces can be directly modelled using a variant of the Horton equation. This is an empirical formula derived from infiltrometer/small catchment studies and is usually expressed as a function of time:

(1) where: ¦ is the potential infiltration rate (mm/hr) ¦0 is the initial infiltration rate (soil water content is zero) (mm/hr) ¦c is the final (limiting) infiltration rate (soil is saturated) (mm/hr) kdecay is an exponent governing the rate of decay of the potential infiltration rate (1/hr) t is equivalent infiltration time

Equation 1 is used to evaluate the change in infiltration when there is effective infiltration range, (i.e. whenever there is some water in the surface). The soil becomes more saturated as more water is infiltrated and the infiltration capacity reduces with time.

To evaluate the change in potential infiltration rate during a time step in a mesh element, the maximum potential infiltration volume is calculated as the integral of the potential infiltration rate curve over the time interval (t2-t1=dt):

(2) where: F is the maximum potential infiltration volume (mm) t* is the initial equivalent infiltration time of the soil

The equivalent infiltration time, t*, will be different for each mesh element, and in effect represents the soil saturation state. For example, when the equivalent infiltration time of an element is zero, the soil is considered completely dry and therefore the potential infiltration rate will be at its maximum level.

If the available water in the surface is higher than the maximum potential infiltration rate, F, the new potential infiltration rate will decay from:

(3)

to:

(4)

If the available water in the surface is lower than the maximum potential infiltration rate, F, the potential infiltration rate, f, of the soil at the end of the time step will be calculated based on the soil moisture content.

The soil water content is a quantity given by the balance of the infiltration volume and the drainage volume of the soil. Therefore, the variation in soil water content is given by:

(5) where: DS is change in soil moisture content (mm) Vi is infiltration volume (mm) Vd is drainage volume (mm)

The drainage capacity of the soil is given by the following function of the infiltration equivalent time:

(6) where: d is drainage capacity (mm/hr)

Therefore, for a given equivalent infiltration time, the soil moisture content, S, can be defined as the integral of the difference between the potential infiltration rate and the drainage capacity of the soil, d:

(7)

The soil water content, S, will reach its maximum value as the equivalent infiltration time tends to infinity. In that situation, the potential infiltration rate, f, equals the discharge capacity, d, and the net contribution to S is null. The maximum value of S is given by:

(8)

To calculate the new potential infiltration rate, f, if the available water in the surface is lower than the maximum potential infiltration volume,. F, the procedure is as follows:

1. Calculate the increment of S:

(9) where: Vs is volume in surface (mm) Vd is given by the integral of the drainage curve over the time interval (dt=t2-t2): (10)

2. From the new value of S, the new value of equivalent infiltration time, t can be obtained from the formula:

(11) where: t is equivalent infiltration time (h)

3. From the new value of t, the new potential infiltration rate will be given by:

(12)

Once an element becomes dry, i.e. there is no water volume available in the surface to infiltrate, the soil will start drying up. The drying process is governed by the recovery rate krecovery.

In this situation, the change in potential infiltration rate in a time step (dt=t2-t1) will be governed by the change in S.

The change in S will be governed by the drainage volume, as there is no infiltration volume:

(13) where: Vd is the drainage volume (mm) given by: (14) where: St1 is the soil water content at time t1 (mm) ¦c is the final (limiting) infiltration rate (soil is saturated) (mm/hr) ¦0 is the initial infiltration rate (soil water content is zero) (mm/hr) krecovery is an exponent governing the rate of recovery of the potential infiltration rate (1/hr) dt is the timestep (hr)

The new potential infiltration rate will be obtained following the procedure shown above in steps 2 and 3.