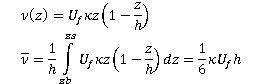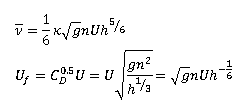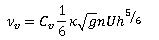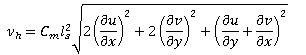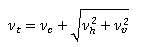Turbulence Model (2D)
Turbulence Model (2D) objects are non-visual objects that are used to define the turbulence characteristics which can be applied to either an entire 2D Zone or to specific Turbulence Zones (2D) in a network.
Turbulence properties are assigned to a 2D Zone and/or one or more Turbulence Zones (2D) by associating a Turbulence Model (2D) with the zone(s).
Turbulence Model (2D) objects can be imported via the Open Data Import Centre or defined on the Polygons Grid or via the Turbulence Zone (2D) Property Sheet. See the Turbulence Model (2D) Data Fields for a description of all the data required to define a Turbulence Model (2D) object.
Once defined, the Turbulence Model (2D) is used to calculate turbulence in 2D elements of a 2D mesh.
A description of how turbulence is modelled is described in the following section.
Turbulence model
Turbulence is accounted for using the eddy viscosity approach following the Boussinesq assumption that the Reynolds stresses or turbulent stresses relate to the main strain tensor of the flow. An additional eddy viscosity is added to the viscous terms in the momentum equations of the shallow water equations to account for the effect of turbulence. The effect of turbulence in the model results will be to dampen the velocity gradients in the solution and therefore dissipate energy.
The eddy viscosity coefficient is calculated using several methods which can be applied globally to a whole 2D Zone or adjusted locally in specific Turbulence Zones (2D). However, the 2D engine only calculates momentum turbulence flows at:
- internal transparent faces (faces without a structure such as a wall, porous wall, or any type of 2D line structure)
- faces connecting elements with turbulence model defined
The eddy viscosity is defined by a combination of the following components:
Vertical eddy viscosity
The vertical eddy viscosity accounts for the turbulence generated by bed friction. On its own it does not account for the effects of horizontal velocity gradients and leads to very low eddy viscosity values when the horizontal gradients are important. Currently, the parabolic model for vertical eddy viscosity is supported.
This model is based on the assumption that the velocity profile over the vertical follows a logarithmic profile, which is a sensible approximation for fully developed turbulent flows. Considering that the flow is at equilibrium, i.e., the hydrostatic pressure forces are balanced by the shear stress over the vertical, the resulting viscosity profile becomes parabolic, and the average value over the vertical becomes:
|
|
where: ν(z) is eddy viscosity (m2/s) U¦ is friction velocity (m/s) K = 0.41: von Karman constant Z is vertical coordinate (m) zs is water surface level (m) zb is bed level (m) h is water depth |
Considering that friction is represented by the Manning empirical formula:
|
|
where: ν is averaged eddy viscosity (m2/s) n is Manning coefficient (s/m1/3) U is Velocity (m/s) |
The final form of the vertical eddy viscosity with the addition of a user defined coefficient becomes:
|
|
where: vv is vertical eddy viscosity (m2/s) Cv is vertical eddy viscosity coefficient |
The value of the vertical eddy viscosity is recalculated for each element every time step as it depends on the hydraulic variables and the bed roughness.
Horizontal eddy viscosity
The horizontal eddy viscosity accounts for the turbulence which occurs as a result of horizontal shear stresses generated by spatial gradients in the velocity field. Two approaches are available:
Mixed length
The horizontal eddy viscosity using the mixed length approach is given by the following formula:
|
|
where: vh is horizontal eddy viscosity (m2/s) Cm is the mixed length coefficient ls = min (0.267 kh, kdw) is characteristic turbulent length scale (m) u is velocity in the x coordinate (m/s) v is velocity in the y coordinate (m/s) |
And the total eddy viscosity is the combination of the constant, the vertical and the horizontal components.
Total eddy viscosity
The total eddy viscosity is calculated from the combination of the constant, the vertical and the horizontal components, and takes the form:
|
|
where: vt is total eddy viscosity (m2/s) vc is constant eddy viscosity (m2/s) vh is horizontal eddy viscosity (m2/s) vv is vertical eddy viscosity (m2/s) |
