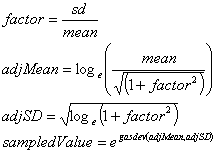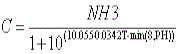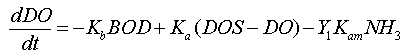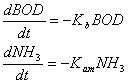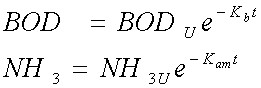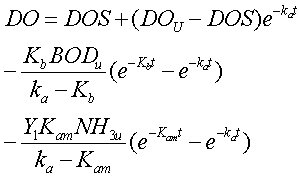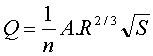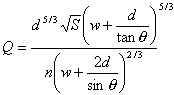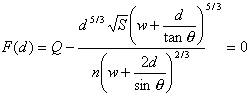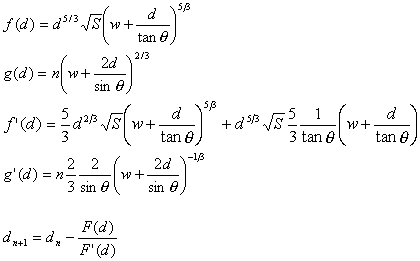UPM Theory
This topic describes the equations used when generating the river impact assessment tables.
Equation for Calculation of Un-ionised Ammonia
Un-ionised ammonia is calculated from:
|
|
where: NH3 is the total ammonia concentration T is the temperature in Celsius PH is the pH level |
Equation for Calculation of Un-ionised Ammonia
The level of dissolved oxygen, total ammonia and BOD are calculated using first order decay equations. The equations used are as follows:
|
|
This is the Streeter\Phelps equation where: Ka is the aeration coefficient Kb is the BOD decay rate (1/days) Kam is the ammonia decay rate (1/days) Y1 is the ammonia yield factor (gO2/gN) DOS is the saturated DO concentration BOD is the BOD concentration NH3 is the total ammonia concentration Ka is given by:
where: U is the stream velocity (m/s) d is the depth (m) C is the Aeration constant vc is the velocity exponent dc is the depth exponent C, vc and dc are set in the UPM River Data dialog - Downstream tab. DOS is given by:
T is the temperature in Celsius PH is the pH level |
DOS is a function of temperature (°C). The calculation of velocity and depth in the downstream river stretch are described in the next section.
This value is fixed downstream.
First order decay equations are used for the change in BOD and change in total ammonia:
|
|
|
Integrating these equations gives:
|
|
These equations are used to calculate the downstream concentrations of BOD and total ammonia where: BODU is upstream BOD concentration (mg/l) NH3U is upstream total ammonia concentration (mg/l) |
Substituting these into the DO equation and integrating yields the equation that is used to calculate the DO concentration downstream:
|
|
where: DOu is the upstream DO concentration (mg/l) |
Note that the equations for BOD, AM and DO downstream are all functions of time t (days).
|
|
where: t is the time (s) X is the length of river stretch (m) U is the velocity through this stretch of river (m/s) |
The calculation of velocity is described in the next section.
Equation for Calculating Velocity and Depth
The simplified equation used to model steady flow using Manning Roughness is:
|
|
where: Q is the flow generated from the log normal distribution (m/s) n is the manning roughness A is the cross-sectional area (m2) R is the hydraulic radius (m) (cross-sectional area of flow divided by perimeter of flow in contact) S is the channel slope (m/m) |
Assuming the channel has a trapezoidal cross section the area is written:
|
|
where: q is the side slope (m/m) d is the depth (m) w is the bottom width |
The flow is therefore written as:
|
|
|
which can be solved for d using an appropriate non-linear equation solver. A Newton-Raphson method has been implemented in InfoWorks ICM.
|
|
|
Newton-Raphson requires the solution of the following equation:
|
|
where:
|
This has been implemented with a default depth estimate of 1.0 m for the first sub-reach. Subsequent sub-reaches use the depth from the previous sub-reach as the initial estimate.
With d known, A can be calculated and the velo,city, U simply equals Q/A.
Sampling from Normal and Log Normal Distributions
The random sampling of a normal distribution has been implemented using a library routine called gasdev(). Essentially the routine takes as input the mean and variance of the required variable and outputs a random sample from the distribution. Although the routine used is implemented in C, equivalent routines exist in well known libraries such as NAG or numerical recipes.
![]()
The random sampling of log normal distributions uses gasdev() with the following modifications/transformations of the mean and standard deviation: