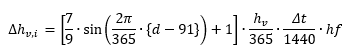DWA (Grenzwertmethode) Runoff Volume Model
This model is based on the runoff volume type suggested from the DWA (German Association for Water, Wastewater and Waste) for pervious and impervious areas called "Grenzwertmethode".
In the Grenzwertmethode, it is assumed from the very start of a rainfall event, that the ground surface (including existing vegetation) receives moisture. After this, the rainfall then starts to infiltrate into the soil (provided the surface is pervious). In the course of the rainfall event, the infiltration capacity and therefore the amount of water infiltrating into the soil decreases due to the increasing soil moisture content. As soon as the rainfall (minus the water used for moistening the ground surface and the water infiltrating into the soil) is larger than zero, a part of the catchment immediately contributes runoff. However, a part of the catchment may not contribute runoff immediately due to, for example, the formation of puddles. In the further course of the rainfall event, the infiltration capacity decreases and the part of the catchment contributing runoff increases exponentially until a certain final percentage is reached. After a rainfall event, the ground surface dries, the infiltration capacity of the soil increases, and the part of the catchment, which would contribute runoff as soon as it starts to rain, decreases again.
Initial conditions and evaporation, can be set in a rainfall event. During a simulation that uses the DWA model, if time varying evaporation has not been specified in the applicable rainfall event, then InfoWorks ICM applies a time varying evaporation factor similar to the one used in the Grenzwertmethode. See the Evaporation section below for further information.
The infiltration part of the InfoWorks ICM's DWA model uses the same runoff volume infiltration as Horton.
To use the DWA (Grenzwertmethode) Model, set the Runoff Volume Type field of the Runoff Surface parameters to DWA.
This model requires the following parameters to be specified:
-
Initial loss value (Vben) - the amount of rainfall necessary to fully moisten the ground surface. For pervious areas, monthly variations are accounted for. See Initial losses for further information.
- Depression loss (Vmuld) - sets the depth of rainfall lost to runoff in depressions (reservoirs). It effectively determines the time between the subcatchment contributing the initial runoff and the subcatchment contributing the maximum amount of runoff. The smaller the depression loss, the shorter the time period between the subcatchment contributing the initial runoff and the subcatchment contributing the maximum amount of runoff.
- Ground slope (IG) - the gradient of a slope (If no gradient or a 0 gradient is specified, InfoWorks ICM uses the gradient defined for the subcatchment).
- Minimum runoff (ѱ0) - a proportion that indicates the amount of runoff the surface will contribute immediately, after the rainfall depth has been reduced by the initial loss and the infiltration loss.
- Maximum runoff (ѱe) - a proportion that indicates the maximum amount of runoff the surface will contribute.
- Initial infiltration (f0), Limiting infiltration (fe), Decay factor (k), and the Recovery factor (k0) - used to calculate the amount of rainfall infiltrating into the soil. See the Horton model for further information.
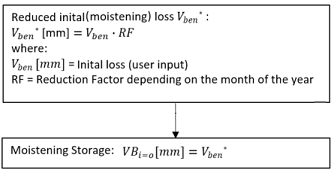
Initial losses and moistening storage
For pervious areas, initial losses also take into consideration the month in which the rainfall event took place. This means that during the winter, the initial loss is smaller than during the summer, which is important in a continuous simulation. The initial loss is determined by the specified Initial loss value * Reduction factor. These factors are suitable for simulations performed for Germany or locations with similar climatic conditions. The reduction factors are as follows:
| Month | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Factor |
0.1 |
0.1 | 0.3 | 0.7 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 0.7 | 0.3 | 0.1 |
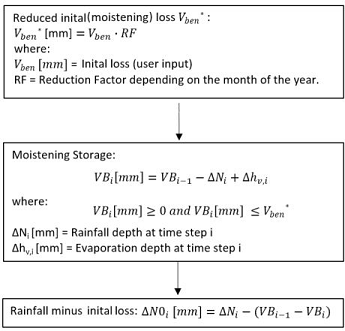
The term, moistening storage, is used to describe the amount of water required to fully moistened the ground surface at each time step. Within a continuous simulation, the recovery of the moistening storage due to evaporation needs to be taken into account. The steps for calculating rainfall minus moistening storage are shown below:
At time step i =0:
At timestep i > 0:
Filling ratio of storage depressions (reservoirs)
Before the first interval, the user specified Depression loss needs to be reduced depending on the ground slope. If the ground slope is ≤ 1 %, the depression loss is not reduced (i.e. reduced depression storage Vmuld* = Vmuld), otherwise the reduced depression loss Vmuld* is:
|
|
Where: IG is the gound slope (%) Vmuld is the depression loss (user input) (mm) |
For example, if the ground slope is 2 %, the reduced depression loss is: Vmuld*=Vmuldx∙e-0.07x2
The filling ratio of the depression must be found for both during rainfall and for periods without rainfall.
During rainfall
The filling ratio of the depression (reservoir) at the end of the interval can be calculated by:
|
|
Where: C (auxillary variable) [-] = (1 - ѱ0)/ Vmuld* ѱ0 is the minimum runoff coefficient (user input) Vmuld* is the reduced depression storage (mm) ΔRi is the rainfall minus initial (moistening) and infiltration loss (mm) |
The filling of the depression can be than calculated by:
|
|
|
As the filling of depression from the previous time step is available for infiltration, it is possible that the rainfall minus moistening and infiltration loss ∆Ri is negative. Finally, the effective rainfall ∆Ai (rainfall minus all losses) can be calculated by:
|
|
Where: C (auxillary variable) [-] = (1 - ѱ0)/ Vmuld* ѱe is the maximum runoff coefficient (user input) Vmuld* is the reduced depression storage (mm) ΔRiis the rainfall minus moistening and infiltration loss (mm) |
During periods without rainfall
If the filling ratio of the previous interval is zero, then the filling ratio of the current interval can also be set to zero. Otherwise, the filling ratio of the depression is related to the potential infiltration depth and the evaporation depth available for emptying the depressions. Due to the exponential approach of the depression filling ratio, the depression never becomes mathematically empty. Therefore, the filling ratio at the end of the current interval (εM,i) is set to zero when the calculated filling ratio multiplied by the reduced depression loss is lower than 0.01, as shown in the following steps:
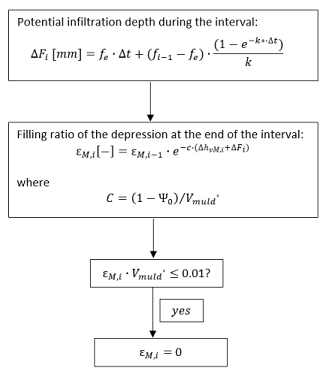
Evaporation
In the DWA Grenzwermethode, a user needs to specify an average yearly evaporation rate, and the evaporation rate at each interval is then calculated using Equation 2, which includes a time varying evaporation factor.
|
|
Where: ∆hv,i = depth of evaporation at interval i hv = average yearly evaporation depth (user input) [mm] d = current day of the year at the time step (e.g. 1st January = 1) (No special rules for leap years) ΔRi is the rainfall minus initial (moistening) and infiltration loss (mm ∆t = duration of the time interval in minutes hf = hourly factor depending on the current hour at the time step given in the following table*:
*The factor only changes at 00:00 hour each day, and then at every hour thereafter. For example, the factor of 0.65 at Hour 7 applies from 07:00:00 to 07:59:59. |
In InfoWorks ICM, the evaporation used in the DWA model can be specified in a rainfall event. If any evaporation profiles were defined on its Evaporation page, then these will be used during simulation without applying the DWA time varying evaporation factor.
However, if no evaporation profiles were defined on the Evaporation page, InfoWorks ICM will apply the DWA time varying factor, shown in Equation 2, to the evaporation rate defined for each rainfall profile in its profile properties (or the sub-event properties if you are using a global value).